単語解説:粘度とは
【はじめに】
今日もあすみ技研レオメーターコラムをご覧いただきありがとうございます。
今回は粘度について書いていきたいと思います。
粘度って何?と突然聞かれてなんとなく流体の流れにくさやドロドロさなどイメージはできるとは思いますが、意外と詳しく説明できる方は少ないのではないでしょうか。
そこで本コラムでは粘度とはどういったものか解説していきたいと思います。
【粘度の定義】
まずは図1のように、ある流体が2枚の板で挟まれ流れているとします。このとき、下の板は固定した状態で上の板をずらすと線上の流体がどのように動いているか考えてみましょう。
まず底面に接している流体は壁面との摩擦により動きません。
次に上面の板に接している流体は、上面の板に引っ張られて一緒に動きます。
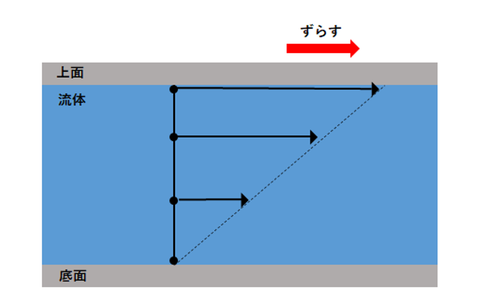
それ以外の部分も含めて、図2にまとめたのでご覧ください。
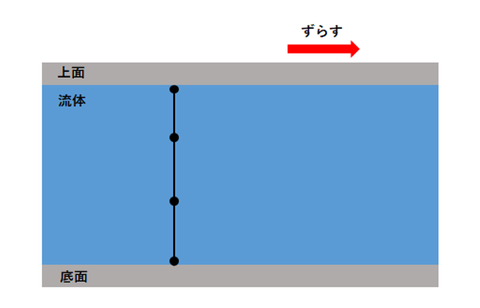
図2で横軸を速度としたグラフとして見たとき、速度側から見た点線の傾きのことを速度勾配といいます。速度勾配は速度(横軸)側から見た傾きのことなので実際に動いている状態を想像していただいたければわかると思いますが、点線が左上側に傾いたときは速度勾配が小さいといい、逆に右下側に傾いたときは速度勾配が大きいといいます。
ここで、ニュートンの粘性法則について少し紹介します。
ニュートンの粘性法則とはニュートンが提示した仮説のようなもので、「流体に対するせん断応力(流体に対して平行にかかる単位面積あたりの力)と速度勾配は比例する。」といった内容です。つまりこれを式にすると、
[せん断応力]= η ×[速度勾配]
となります。ここで出てきた係数ηのことを粘度もしくは粘性係数といいます。
粘度ηが大きいと、ある速度で流体をずらしたいとき大きなせん断応力が必要、つまりその流体はドロドロで
逆に粘度ηが小さいと、小さなせん断応力で流体を同じ速度でずらせる、つまりその流体はサラサラというように、
粘度ηは流体の粘り気の指標となります。
また、詳しい内容は省略しますが、速度勾配はせん断変形が微小な時、せん断速度とイコールの関係が成り立ちますので、
[粘度η]=[せん断応力]/[せん断速度]
このように表すこともできます。
【ニュートン流体と非ニュートン流体】
ここまでで示したようにせん断応力とせん断速度が比例する、つまり速くずらすためにはそれに比例して大きな力が必要になるような流体のことをニュートン流体といい、この比例関係に当てはまらない流体のことを非ニュートン流体といいます。
次のコラムでは非ニュートン流体について書いていきますので、気になる方はぜひ読んでみてください。
それでは最後までお読みいただきありがとうございました。
(M.H)

